Description
La maquette du système solaire, ou planétaire, comporte :
- Une planche de base : fond de ciel étoilé avec le soleil au centre et, en périphérie, une graduation de 0 à 360° dans le sens inverse des aiguilles d'une montre. L'origine est le point vernal gamma : c'est la direction du Soleil vu de la Terre à l'équinoxe de printemps. Ce plan est celui du système solaire (les orbites des planètes ne sont pas coplanaires, mais les inclinaisons étant faibles, on peut négliger ce fait). La graduation donne la longitude héliocentrique, angle entre le point gamma, le Soleil et la planète. Elle permet de positionner à une date donnée la planète sur sa trajectoire et est donnée par les éphémérides.
Vocabulaire
Les planètes plus éloignées du Soleil que la Terre sont appelées planètes supérieures (Mars, Jupiter, Uranus, Neptune). Les planètes plus proches du Soleil que la Terre sont les planètes inférieures (Mercure et Vénus).
On appelle élongation d'une planète l'angle Soleil-Terre-planète. C'est l'angle entre le Soleil et la planète vu depuis la Terre.
Cas A : Jupiter, une planète supérieure
On
place sur le fond
étoilé le disque A1 (Jupiter sur son orbite) puis
le
disque A2 (la Terre sur son orbite). Les distances relatives
Soleil-planète sont respectées : Jupiter est 5
fois plus
éloigné du Soleil que la Terre. On recherche les
longitudes héliocentriques dans les
éphémérides et on place la Terre et
Jupiter
à une date donnée.
Voici une photo de ce que vous devriez obtenir.
Pour faire tourner la Terre et Jupiter sur leur orbite, il faut calculer l'angle parcouru par chaque planète en un intervalle de temps donné. La Terre tourne autour du Soleil en 1 an, Jupiter en 11,86 ans. Ainsi, quand la Terre parcourt 15° sur son orbite, Jupiter parcourt 15/11,86 = 1,3°. On peut ainsi faire tourner les planètes autour du Soleil et trouver à quelles dates elles se trouvent dans des configurations caractéristiques.
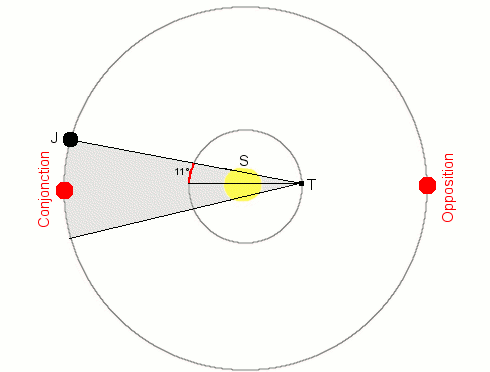
Deux configurations caractéristiques sont indiquées : l'alignement Jupiter-Terre-Soleil (opposition, la Terre et Jupiter ont la même longitude héliocentrique) et l'alignement Jupiter-Soleil-Terre (conjonction, l'écart entre les longitudes héliocentriques de la Terre et de Jupiter vaut 180°). Dans le premier cas, Jupiter est opposé au Soleil et est bien visible dans le ciel nocturne où il culmine en milieu de nuit. Dans le deuxième cas, Jupiter est derrière le Soleil et est invisible. Pour que Jupiter soit visible au crépuscule, son élongation doit être au-moins égal à 11°. On pourra poser un cercle en papier calque sur la maquette et tracer ce cône d'invisibilité. On peut alors repérer les longitudes héliocentriques de Jupiter quand il rentre et sort de ce cône, et en déduire la durée d'invisibilité de Jupiter avec les éphémérides.
Cas B : Vénus, une planète inférieureVoici une photo de ce que vous devriez obtenir.
Pour faire tourner la Terre et Jupiter sur leur orbite, il faut calculer l'angle parcouru par chaque planète en un intervalle de temps donné. La Terre tourne autour du Soleil en 1 an, Jupiter en 11,86 ans. Ainsi, quand la Terre parcourt 15° sur son orbite, Jupiter parcourt 15/11,86 = 1,3°. On peut ainsi faire tourner les planètes autour du Soleil et trouver à quelles dates elles se trouvent dans des configurations caractéristiques.
Deux configurations caractéristiques sont indiquées : l'alignement Jupiter-Terre-Soleil (opposition, la Terre et Jupiter ont la même longitude héliocentrique) et l'alignement Jupiter-Soleil-Terre (conjonction, l'écart entre les longitudes héliocentriques de la Terre et de Jupiter vaut 180°). Dans le premier cas, Jupiter est opposé au Soleil et est bien visible dans le ciel nocturne où il culmine en milieu de nuit. Dans le deuxième cas, Jupiter est derrière le Soleil et est invisible. Pour que Jupiter soit visible au crépuscule, son élongation doit être au-moins égal à 11°. On pourra poser un cercle en papier calque sur la maquette et tracer ce cône d'invisibilité. On peut alors repérer les longitudes héliocentriques de Jupiter quand il rentre et sort de ce cône, et en déduire la durée d'invisibilité de Jupiter avec les éphémérides.

On
place sur le fond
étoilé le disque B1 (la Terre sur son orbite)
puis
le disque B2 (Vénus sur son orbite). Les distances relatives
Soleil-planète sont respectées :
Vénus-Soleil =
0,72 x Terre-Soleil. On recherche les longitudes
héliocentriques
dans
les éphémérides et on place la Terre
et
Vénus
à une date donnée.
Voici une photo de ce que vous devriez obtenir.
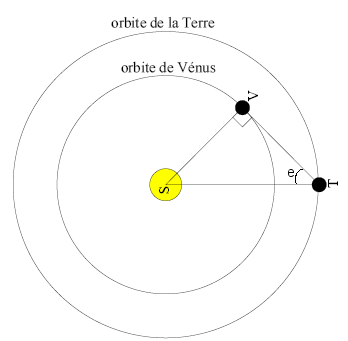
Contrairement aux planètes supérieures dont l'élongation peut varier entre 0° et 180°, il existe une élongation maximale pour les planètes inférieures : vues depuis la Terre, elles ne peuvent pas s'éloigner du Soleil d'un angle plus grand que cette élongation. Pour cette raison, Vénus et Mercure sont toujours proches du Soleil dans le ciel. On peut les voir soit le matin peu avant le lever du Soleil, soit le soir peu après le coucher du Soleil, mais jamais en milieu de nuit. Lorsque Vénus est à son élongation maximale, la ligne Terre-Vénus est tangente à l'orbite de Vénus. Ces tangentes sont représentées sur le disque B1.
Calcul de l'élongation maximale e de Vénus :
 Elongation
maximale
Elongation
maximale
Pour faire tourner la Terre et Vénus sur leur orbite, il faut calculer l'angle parcouru par chaque planète en un intervalle de temps donné. La Terre tourne autour du Soleil en 1 an, Vénus en 225 jours, soit 0,62 an. Ainsi, quand la Terre parcourt 15° sur son orbite, Vénus parcourt 10/0,62 = 24,2°. On peut ainsi faire tourner les planètes autour du Soleil et trouver à quelles dates elles se trouvent dans des configurations caractéristiques.
Voici une photo de ce que vous devriez obtenir.
Contrairement aux planètes supérieures dont l'élongation peut varier entre 0° et 180°, il existe une élongation maximale pour les planètes inférieures : vues depuis la Terre, elles ne peuvent pas s'éloigner du Soleil d'un angle plus grand que cette élongation. Pour cette raison, Vénus et Mercure sont toujours proches du Soleil dans le ciel. On peut les voir soit le matin peu avant le lever du Soleil, soit le soir peu après le coucher du Soleil, mais jamais en milieu de nuit. Lorsque Vénus est à son élongation maximale, la ligne Terre-Vénus est tangente à l'orbite de Vénus. Ces tangentes sont représentées sur le disque B1.
Calcul de l'élongation maximale e de Vénus :
sin
e =
Soleil-Vénus/Soleil-Terre = 0,72
e
= 46°
 Elongation
maximale
Elongation
maximalePour faire tourner la Terre et Vénus sur leur orbite, il faut calculer l'angle parcouru par chaque planète en un intervalle de temps donné. La Terre tourne autour du Soleil en 1 an, Vénus en 225 jours, soit 0,62 an. Ainsi, quand la Terre parcourt 15° sur son orbite, Vénus parcourt 10/0,62 = 24,2°. On peut ainsi faire tourner les planètes autour du Soleil et trouver à quelles dates elles se trouvent dans des configurations caractéristiques.
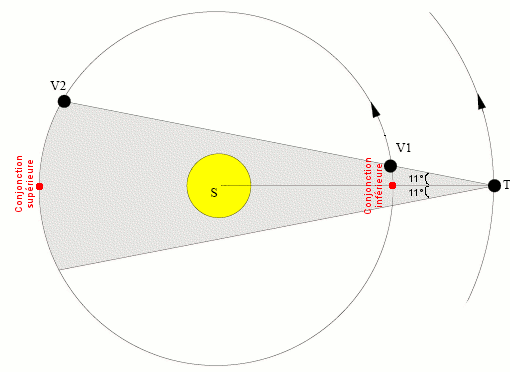
Outre
les élongations
maximales, deux configurations
caractéristiques sont indiquées : la conjonction
inférieure
(alignement Terre-Vénus-Soleil, même longitude
héliocentrique) et la conjonction
supérieure
(alignement Terre-Soleil-Vénus,
écart de 180° entre les longitudes
héliocentriques).
Dans les deux cas, Vénus se trouve dans la même
direction
que le Soleil, soit devant, soit derrière. Dans les deux
cas,
elle est invisible. A nouveau, on peut tracer sur un calque le
cône d'invisibilité (Vénus devient
visible lorsque
son élongation est supérieure à
11°) et en
déduire les durées d'invisibilité
(environ 15
jours autour de la conjonction inférieure et 88 jours autour
de
la conjonction supérieure).

Cas C : La Terre, Vénus et Mars
On
place sur le fond
étoilé le disque C1 (Mars sur son orbite),
le disque C2 (la Terre sur son orbite), puis
le disque C3 (Vénus sur son orbite). Les distances relatives
Soleil-planète sont respectées : Mars-Soleil =
1,5 x
Terre-Soleil et Vénus-Soleil = 0,72 x Terre-Soleil. Les
planètes sont représentées par des
billes que l'on
place dans une alvéole. On recherche les longitudes
héliocentriques dans
les éphémérides et on place la Terre,
Mars et
Vénus à une date donnée. Pour faire
tourner les
planètes autour du Soleil, on les déplace en
même
temps dans les alvéoles successives dans le sens inverse des
aiguilles d'une montre. Deux alvéoles successives
correspondent
au déplacement sur 15 jours.
Voici une photo de ce que vous devriez obtenir (il manque la bille rouge de mars sur cette photo)
On peut voir ainsi l'évolution des positions des planètes au cours du temps, et repérer, en particulier les conjonctions et oppositions pour Mars, les conjonctions inférieures et supérieures pour Vénus, les conjonctions Mars-Vénus (alignement Terre-Vénus-Mars, Vénus et Mars ont alors la même longitude héliocentrique et se trouvent proches l'une de l'autre dans le ciel nocturne).
Document
d'accompagnement : Voici une photo de ce que vous devriez obtenir (il manque la bille rouge de mars sur cette photo)
On peut voir ainsi l'évolution des positions des planètes au cours du temps, et repérer, en particulier les conjonctions et oppositions pour Mars, les conjonctions inférieures et supérieures pour Vénus, les conjonctions Mars-Vénus (alignement Terre-Vénus-Mars, Vénus et Mars ont alors la même longitude héliocentrique et se trouvent proches l'une de l'autre dans le ciel nocturne).
- La troisième loi de Kepler
| Planète |
angle |
T |
| Terre |
15° |
360° x 15jours/15° = 360 jours ~ 1 an |
| Vénus |
24° |
360° x 15jours/24° = 225 jours |
| Mars |
8° |
360° x 15jours/8° = 675 jours ~ 1,85 an |
On
peut ensuite calculer le rapport
(distance Soleil-planète)3
/ T2
et constater qu'il est constant : il s'agit de la troisième
loi
de Kepler.
| Planète |
T
(an) |
distance
relative d |
d3 / T2 |
| Terre |
1 |
1 |
1 |
| Vénus |
0,62 |
0,72 |
0,97 ~ 1 |
| Mars |
1,85 |
1,5 |
0,99 ~ 1 |
Lecture du planétaire